Calculate paths between nodes in an Optimal Channel Network

Function that determines upstream and downstream paths and path lengths between any nodes of the network at the aggregated level.

Usage

paths_OCN(OCN, level = c("RN","AG"), whichNodes = NULL, includePaths = FALSE, 
includeDownstreamNode = FALSE, includeUnconnectedPaths = FALSE, displayUpdates = FALSE)

Arguments

OCN: A river object as produced by aggregate_OCN.
level: Character vector. At which level should paths be calculated? Possible values are "RN", "AG", or both.
whichNodes: List. It allows specifying a subset of nodes for which paths are computed. In the case of large rivers, this could speed up the function execution substantially. It must contain objects named RN and/or AG. Each of these objects is a vector with the indices of the nodes for which paths are to be calculated. Default is NULL, which leads to calculation of paths between all nodes at the level(s) specified in level. If whichNodes contains a single object (RN or AG), this is taken as the level at which paths are calculated (i.e., level is overwritten). If not present, the outlet node is automatically added. See example.
includePaths: Logical. If TRUE, RN$downstreamPath and AG$downstreamPath are included to the output object. Note that this might slow down the function execution considerably, and create RAM issues for very large OCNs.
includeDownstreamNode: Logical. If TRUE, path lengths include the length of the edge departing from the last downstream node of the path.
includeUnconnectedPaths: Logical. If TRUE, calculate path lengths between unconnected nodes (RN$downstreamLengthUnconnected and AG$downstreamLengthUnconnected). Note that this might slow down the function execution considerably, and create RAM issues for very large OCNs.
displayUpdates: Logical. State if updates are printed on the console while paths_OCN runs.

Value

A river object that contains all objects contained in OCN, in addition to the objects listed below.

RN$downstreamPath: List (of length OCN$RN$nNodes) whose object i is a list (of length OCN$RN$nNodes). If nodes i and j are connected by a downstream path, then RN$downstreamPath[[i]][[j]] is a vector containing the indices of the nodes constituting such path (i and j are included). If i and j are not connected by a downstream path, then RN$downstreamPath[[i]][[j]] = NULL. Only present if includePaths = TRUE.
RN$downstreamPathLength: Sparse matrix (OCN$RN$nNodes by OCN$RN$nNodes) containing length of paths between nodes that are connected by a downstream path; if i and j are not connected by a downstream path, then RN$downstreamPathLength[i,j] = 0. Note that RN$downstreamPathLength[i,i] = 0 if includeDownstreamNode = FALSE; alternatively, it is RN$downstreamPathLength[i,i] = OCN$RN$leng[i]. It is a spam object.
RN$downstreamLengthUnconnected: Matrix (OCN$RN$nNodes by OCN$RN$nNodes). RN$downstreamLengthUnconnected[i,j] is the length of the downstream portion of a path joining node i to j if i and j are not connected by a downstream path. Specifically, RN$downstreamLengthUnconnected[i,j] = RN$downstreamPathLength[i,k], where k is a node such that there exist a downstream path from i to k and from j to k, and these paths are the shortest possible. Note that the length of the upstream portion of the path joining i to j is given by RN$downstreamLengthUnconnected[j,i]. If instead i and j are joined by a downstream path, then RN$downstreamLengthUnconnected[i,j] = 0. Only present if includeUnconnectedPaths = TRUE.
AG$downstreamPath: List (of length OCN$AG$nNodes) whose object i is a list (of length OCN$AG$nNodes). If nodes i and j are connected by a downstream path, then AG$downstreamPath[[i]][[j]] is a vector containing the indices of the nodes constituting such path (i and j are included). If i and j are not connected by a downstream path, then AG$downstreamPath[[i]][[j]] = NULL. Only present if includePaths = TRUE.
AG$downstreamPathLength: Sparse matrix (OCN$AG$nNodes by OCN$AG$nNodes) containing length of paths between nodes that are connected by a downstream path; if i and j are not connected by a downstream path, then AG$downstreamPathLength[i,j] = 0. Note that AG$downstreamPathLength[i,i] = 0 if includeDownstreamNode = FALSE; alternatively, it is AG$downstreamPathLength[i,i] = OCN$AG$leng[i]. It is a spam object.
AG$downstreamLengthUnconnected: Matrix (OCN$AG$nNodes by OCN$AG$nNodes). AG$downstreamLengthUnconnected[i,j] is the length of the downstream portion of a path joining node i to j if i and j are not connected by a downstream path. Specifically, AG$downstreamLengthUnconnected[i,j] = AG$downstreamPathLength[i,k], where k is a node such that there exist a downstream path from i to k and from j to k, and these paths are the shortest possible. Note that the length of the upstream portion of the path joining i to j is given by AG$downstreamLengthUnconnected[j,i]. If instead i and j are joined by a downstream path, then AG$downstreamLengthUnconnected[i,j] = 0. Only present if includeUnconnectedPaths = TRUE.

Examples

# 1) Calculate paths between nodes of an OCN
OCN <- paths_OCN(aggregate_OCN(landscape_OCN(OCN_20), thrA = 4))
# \donttest{
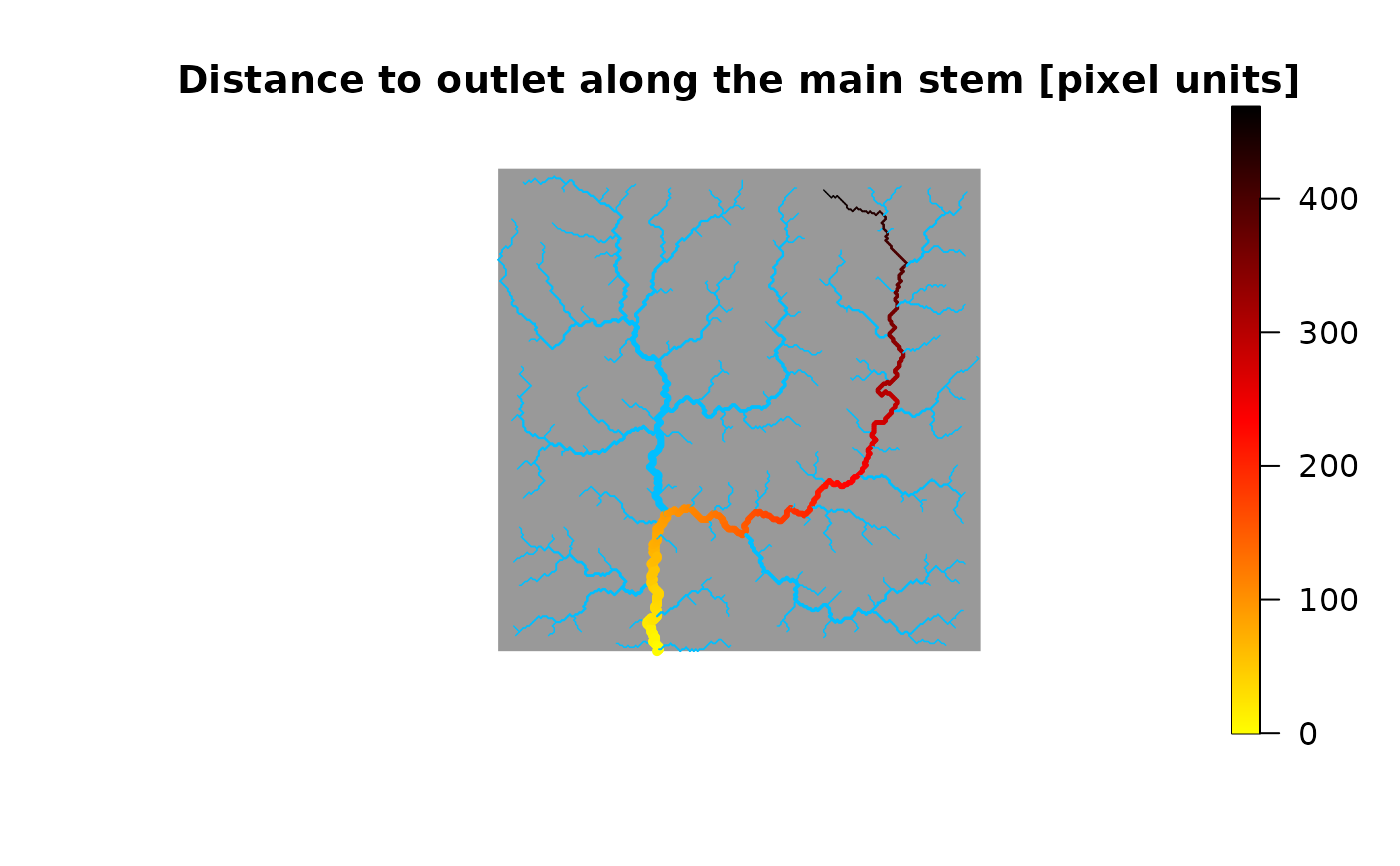
# 2) Display distance to outlet (at the RN level) along the main stem
# of an OCN
OCN <- aggregate_OCN(landscape_OCN(OCN_250_T)) # this takes some seconds
OCN <- paths_OCN(OCN, includePaths = TRUE) # this takes some seconds

distanceToOutlet <- OCN$RN$downstreamPathLength[,OCN$RN$outlet]
farthestNode <- which(distanceToOutlet == max(distanceToOutlet))
mainStem <- OCN$RN$downstreamPath[[farthestNode]][[OCN$RN$outlet]]
theme <- rep(NaN, OCN$RN$nNodes)
theme[mainStem] <- distanceToOutlet[mainStem]

draw_thematic_OCN(theme, OCN)
title("Distance to outlet along the main stem [pixel units]")


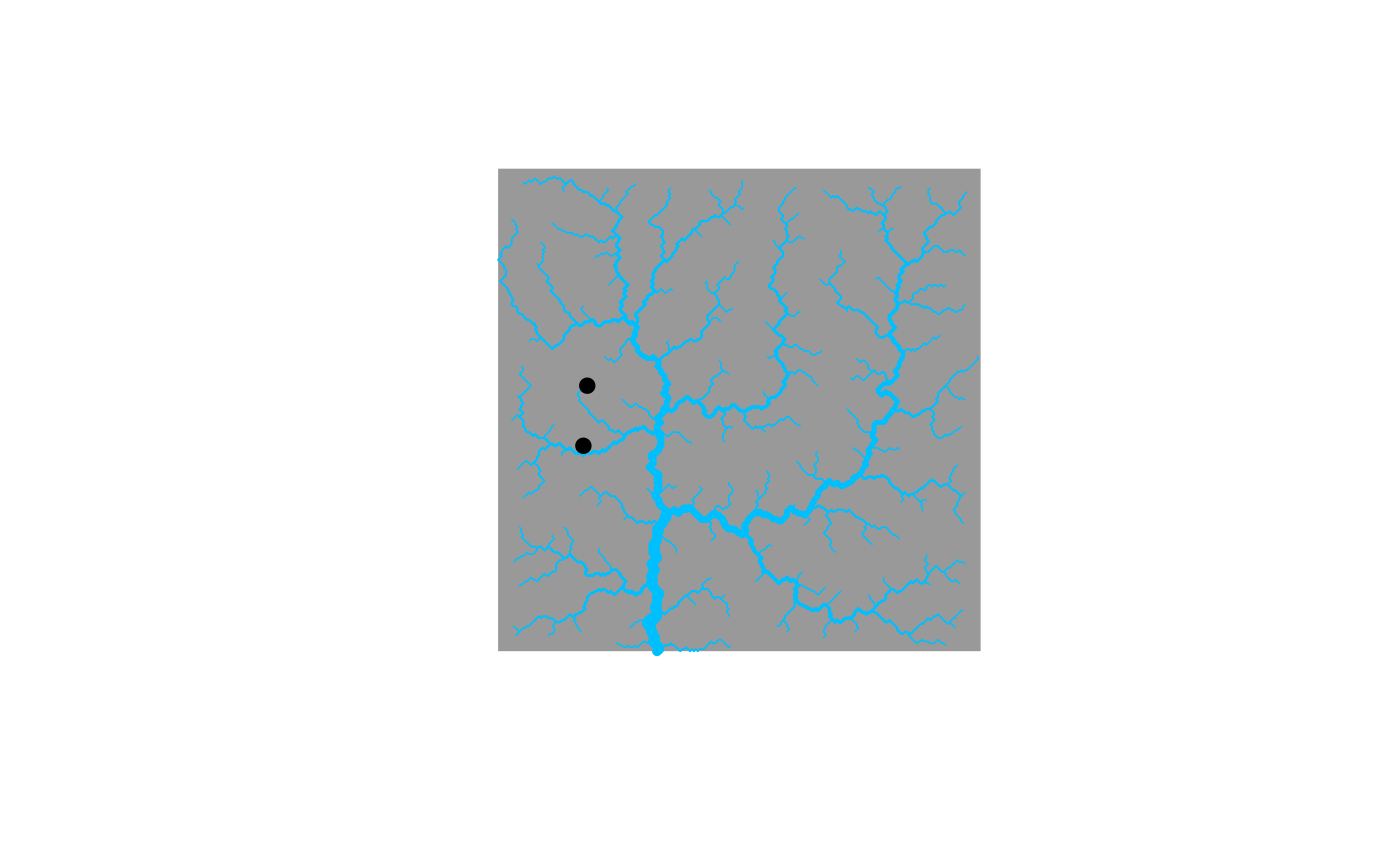
# 3) use whichNodes to compute distance between two non flow-connected nodes 
OCN <- aggregate_OCN(landscape_OCN(OCN_250_T)) # this takes some seconds
RNnodes <- c(483, 516)
plot(OCN)
points(OCN$RN$X[RNnodes], OCN$RN$Y[RNnodes], pch = 19) # nodes 483 and 516 are not flow-connected

OCN <- paths_OCN(OCN, whichNodes = list(RN=RNnodes), includePaths = TRUE,
         includeUnconnectedPaths = TRUE)
OCN$RN$downstreamPath[[RNnodes[1]]][[OCN$RN$outlet]] 
#>   [1]  483  500  514  513  524  534  542  550  561  575  587  598  611  623  636
#>  [16]  651  662  674  689  712  734  758  779  780  796  811  822  831  840  852
#>  [31]  867  881  890  898  907  918  930  954  984 1015 1051 1082 1105 1081 1104
#>  [46] 1103 1102 1101 1100 1080 1079 1050 1014  983  953  952  982  981  980  951
#>  [61]  929  950  979 1013 1049 1078 1077 1048 1076 1047 1075 1074 1046 1073 1045
#>  [76] 1012 1011 1044 1072 1071 1070 1098 1123 1149 1171 1170 1148 1169 1147 1122
#>  [91] 1121 1097 1068 1042 1067 1041 1040 1039 1038 1037 1009  976 1008  975 1007
#> [106]  974 1006 1036 1035 1005  973  946  972  971 1004  970  969  945  944  968
#> [121]  943  942  967  966 1003 1034 1065 1064 1033 1032 1031 1030 1029 1002 1001
#> [136] 1028 1027 1026 1025 1000  965  941  925  914  913  924  940  939  938  964
#> [151]  963  999  998  962  997 1024 1062 1061 1023
# the outlet node has been added to whichNodes$RN
OCN$RN$downstreamLengthUnconnected[RNnodes[1], RNnodes[2]] 
#> [1] 30.04163
# distance from node 1 to the common downstream confluence
OCN$RN$downstreamLengthUnconnected[RNnodes[2], RNnodes[1]] 
#> [1] 44.35534
# distance from node 2 to the common downstream confluence
# }